A matrix approach to the Moog ladder filter

[mystran]

But when you really push the input gain, the output waveform gets more "spiky." This is true no matter how high you push the oversampling.

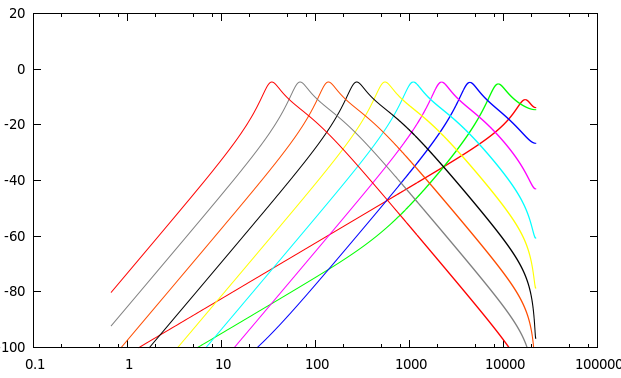
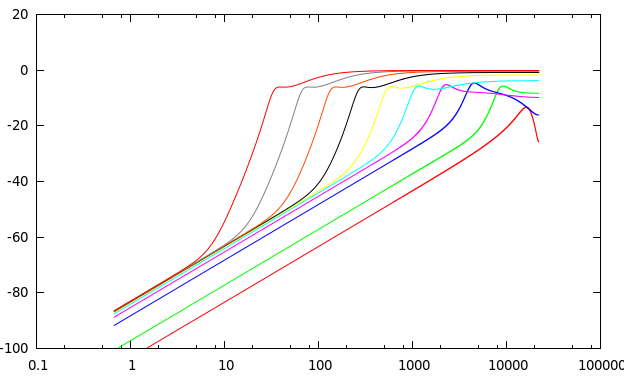
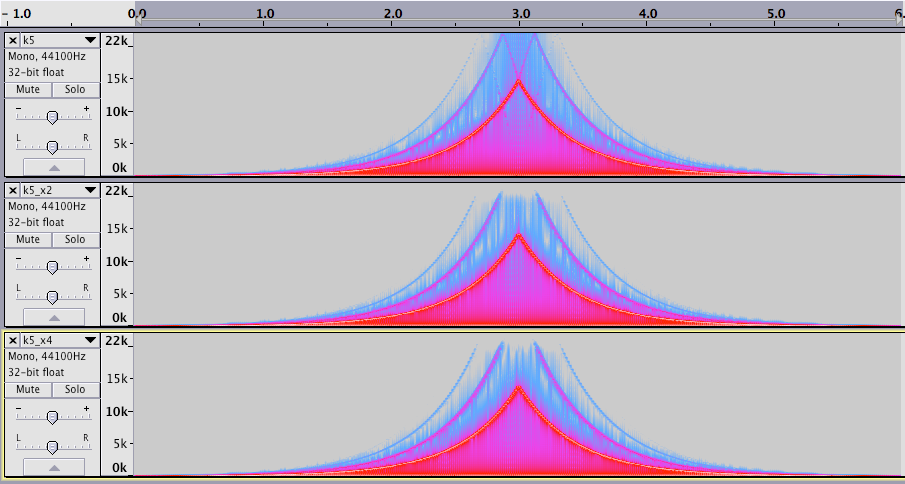
The spiking is expected behavior: the previous sound under-estimates the attenuation required for the next sample. Proper oversampling helps in two ways: the up-sampling filter will make the input smoother, and most of the spikes will be at higher frequencies, so the down-sampling will filter them out.

If you aren't getting any improvement with oversampling, then I suspect you are taking some unsafe short-cuts (like not using proper filtering both ways). There will certainly be Gibbs spikes from the down-sampling, but that's different and expected from any method.

That said, you need pretty silly over-sampling for high-gain situations. If that's what you want to do, then this is not a good approach. Note that the tanh(x)/x approximation that I proposed doesn't work for high-gain either, so you would also need to improve that one.

My general feeling (no proof) is that mystran's approach should work better for not-so-extreme settings, whereas the cheapest approach should deliver better results at the extremes.

I actually recently found out that some pre-historic (pre-SPICE) circuit simulator apparently used (with iteration) a scheme very similar to what I proposed.

But.. yes, I designed it to be "the most simple thing that could work" for the case where you can get reasonable results without iteration. For high-gain situations you want iteration, and then it makes sense to switch to Newton instead, which only costs marginally more per iteration, generally converges much faster, and kinda benefits more from oversampling too.

As for simply altering the solution, yeah that's cheap, but IIRC you can run into problems if you don't clip the state-variables, and clipping the state-variable isn't quite the right thing (so you're not really solving the right system).

There's also the "cheapest" approach, which simply applies nonlinearities on top of the zero-delay feedback solution (without attempting to use any "history" data).

It is not obvious to me how one would do this while still solving the same system. Do you mean like solving the currents, estimating what the resulting voltages would be, applying the non-linearities and then estimating the currents again from those (and integrating those) or what?

Care to provide some links if this was discussed somewhere?

I know you can also just clip the state-variables or some such similar thing, but that isn't really the same filter anymore then..

[Z1202]

There's also the "cheapest" approach, which simply applies nonlinearities on top of the zero-delay feedback solution (without attempting to use any "history" data).

It is not obvious to me how one would do this while still solving the same system. Do you mean like solving the currents, estimating what the resulting voltages would be, applying the non-linearities and then estimating the currents again from those (and integrating those) or what?

Care to provide some links if this was discussed somewhere?

Basically this is my version of the "cheap" approach I was advocating all the time in the article and in the book. But maybe I didn't describe it in enough details, thinking that this approach is quite obvious. I think a similar approach is also mentioned by the simulanalog guys in their article (they compare its results against proper Newton-Raphson solution, IIRC).

Suppose we use a ladder filter with a single saturator at the feedback point. We can solve the linear zero-delay equation for this point. Then apply the saturator to this value, thereby obtaining the saturator's output value and simply proceed updating the 1-pole filter states using the known input values. [Edit: if you have Reaktor, exactly this kind of implementation is uploaded to the user library as the "tutorial solution". If you don't have it, the tutorial accompanying the article may give more insights nevertheless.]

If there are several nonlinearities, the process may get more complicated, but still nothing too esoteric. I don't have a fully formal description, but I guess you get the idea.

The beauty of this approach is that it works more or less "equally bad" at moderate and at extreme settings, whereas iterative approaches seem to have more and more problems, the more you get into the extreme areas. E.g. Newton-Raphson converges slower and slower as you raise the feedback and the cutoff.

Edit: sorry, the links.
The tutorial (particularly see Fig.5)
http://www.native-instruments.com/filea ... logyRC.pdf
The article (the first paragraph at p.5)
http://www.native-instruments.com/filea ... pology.pdf
The book (first paragraph at p.67)
http://www.native-instruments.com/filea ... _1.0.3.pdf
Reaktor patches (available if you officially own Reaktor license)
http://co.native-instruments.com/index. ... tchid=7775

Edit: it almost seems to me, as if the thread was hijacked, as we drifted from the matrix exponential filter discussion and comparing those to TPT BLT to almost pure discussion of TPT BLT. Maybe we should move this to another thread? E.g. mystran's method thread?

[raphx]

Duh, the spikiness I was seeing was because of the tanh/x approximation. If I plug in the real tanh, it converges nicely - at 8x oversampling, you can pretty much lay the waveforms on top of each other.

It took me a few tries, but I was able to combine nonlinearity with the original TPT approach. Basically, I used the linear solution, did the saturations (including xin - r * s[3]), then wrote everything following that in terms of the saturated values. I think this is the same as what Vadim was proposing.

With the matrix approach, each new value depends only on the state variables from the previous iteration. Thus, you don't need anything resembling Newton-Raphson iteration.

BTW, I'm fine with some discussion of the TPT in this thread. It's clearly a very good solution and likely still the best for audio-rate modulation. It makes sense to understand it fully as a basis of comparison, especially before I go off and make any more foolish claims.

At this point, I'm seeing very comparable quality from the three approaches. So I think the main basis for choosing one or the other is performance. Again, I'll back this up with hard data when I get it.

[Z1202]

With the matrix approach, each new value depends only on the state variables from the previous iteration. Thus, you don't need anything resembling Newton-Raphson iteration.

But you can't plug the nonlinearities into the squared matrix, can you? As I understood your paper, you were applying the nonlinearities outside of the "folded" iterative linear matrix multiplication process, kinda similar to the "cheap" approach I was talking about. Did I misunderstand something?

BTW, I wonder how the deviations of the phase response in your approach will affect the modes of the ladder filter (BP, HP, etc). For BLT you generally don't bother with that kind of question, since the relationship between the amplitude and the phase is fully preserved there.

[raphx]

Z1202: I think it is basically the same as your "cheap" approach. In each step, you apply the nonlinear functions to all state variables and the input, then you multiply these by the transition matrix to create a delta update (so the identity matrix is subtracted from the Expm solution), in such a way that it's identical to the linear solution under the assumption that your sigmoid is identity.

The quick answer regarding the other modes is that it works beautifully for bandpass except at the very highest frequencies, but not so well for highpass.





It should definitely be possible to recover the highpass response by adding a FIR with carefully matched phase response to replace the sample-and-hold assumption, essentially the same technique as Särkkä and Huovilainen's "Accurate Discretization of Analog Audio Filters With Application to Parametric Equalizer Design". This will add some complexity and cost, however, where as you point out there is no special problem with the BLT.

[mystran]

Thanks Z1202 for the throughout post, though shorter would have been enough.

As for Newton, you can sometimes speed it up by solving the inverse problem instead (and you can switch strategies on the fly for each iteration and each non-linearity separately). Unfortunately getting it to work is difficult enough that I don't really feel qualified to try to explain the details.

But I agree that's not necessarily very relevant to the original topic (especially as such things make little sense unless you're shooting for quality and willing to significantly raise the CPU cost).

[mystran]

Duh, the spikiness I was seeing was because of the tanh/x approximation. If I plug in the real tanh, it converges nicely - at 8x oversampling, you can pretty much lay the waveforms on top of each other.

With the matrix approach, each new value depends only on the state variables from the previous iteration. Thus, you don't need anything resembling Newton-Raphson iteration.

Out of curiosity, how well does it work in forced self-oscillation or with positive feedback?

[raphx]

mystran: In both cases (I tried k=5 and k=-1) it seems to solve the equations. For k=-1, even 1x and 2x oversampling sound and look pretty similar, because that setting seems to be emphasizing the lowpass.

From everything I've seen so far, the gold standard for quality is increasing the oversampling rate, as opposed to fancy tricks with Newton iteration or whatnot. If you're driving the input with high level, high frequency sine waves, the aliasing doesn't really go away until 8x or 16x. And by that time the accuracy of any of the three contenders as far as frequency response and nonlinear waveshape is so good I don't think anyone would be able to tell the difference. So, in my opinion anyway, it all comes down to performance. Even when you are updating parameters at a high rate, for extreme levels of oversampling the matrix exponential approach may still come out ahead because of how fast it can crank the kernel.

[Z1202]

OK, next question: although the general formula for a matrix exponential requires either summation of infinite series or transformation to the Jordan normal form, maybe in the particular case of the ladder filter there is a reasonably simple analytical expression for the limiting case?

[mystran]

mystran: In both cases (I tried k=5 and k=-1) it seems to solve the equations. For k=-1, even 1x and 2x oversampling sound and look pretty similar, because that setting seems to be emphasizing the lowpass.

Well, that much was kinda obvious. So let me rephrase for a more specific question: what does the sine-purity look like with self-oscillation at high frequencies? Does the wave-shape stay (roughly) the same as you sweep the cutoff?

From everything I've seen so far, the gold standard for quality is increasing the oversampling rate, as opposed to fancy tricks with Newton iteration or whatnot.

Newton iteration isn't a fancy trick though. In general how you solve non-linearities is orthogonal to the integration method (whether implicit or explicit) and in fact you usually need some such method even for solving DC circuits (ie all capacitors disconnected, all inductors shorted.. in terms of DSP this comes down to removing all integrators), unless there is a strict "one way only" signal flow (which I would call a "happy special case").

In fact, whether you use an implicit or explicit integration, the Newton in general looks pretty much the same. The Jacobian will look different depending on the integration method, but otherwise it's the same. If all the non-linear functions are scalar to scalar and there are delays in the signal-flow between each of them (so they aren't connected in the "instant" sense), then the Jacobian (and it's inverse obviously) will be diagonal (or you can make it so). In this case there might be an analytic solution as well (but often times there is not.. for example a diode in series with a resistor will give you a system for which the analytic "solution" is useless).

Now with the Moog ladder with feedback tanh() and explicit integration, we have the happy special-case where there is delay in the feedback path of the non-linearity, so you can simply calculate it as a function. Unfortunately it's not quite that simple if you want to do composition on the system.

See, linear function f can be represented as a matrix F and the function composition can be done by matrix multiplication, so f(f(x))) = F*F*x and so on. For the point of a mental exercise, let's assume there is a function type T such that for f and g in T, a and b in R, we have f*f as the function composition, f*a = f(a), a*f*b = a*f(b), (f+g)*a = f(a)*g(a), f*g*a=f(g(a)) and so on (assuming I got it right, this should match matrices for the linear case, if not, assume it does). Then we can plug the tanh into the matrix, and calculate the exponential with the power-series, etc.

Trouble is, where as with the original matrix the tanh is simply a term in the last column of the first row (for the state-space order from OP), the exponentiation will spread it's powers and evaluations everywhere. So we can't really do such cheap composition anymore (well, until someone invents hardware that can do arithmetic on non-linear functions). So instead we need to pretend that for the duration of the composite step, the function is something we can represent in the matrix (which is another way to say "the function is linear").

This gets us back to Newton, which essentially amounts to approximating the function f(x1) by f(x0)+(x1-x0)*f'(x0) and then iterating until x1-x0=0, or close enough (or f(x1)-f(x0) is less than some tolerance). This approximation is now linear, so it can happily live as a coefficient (or sub-matrix for multi-variate) in the numeric matrix, and composition works again. So we can exponentiate the resulting state-space, solve for the estimate, then refine the approximation and iteration until converge [footnote: doing it this way is realistic for implicit linear multi-step methods, because you can put the Newton-iteration in the middle of the factorization to only solve everything else once, but I'm not seriously suggesting you do it like that for exponentiation].

Obviously instead of linearizing at the target point, you can linearize at the starting point (at the old value of x). This way you get rid of all iteration if the "happy special-case" happens to hold. Even if not, you only need to iterate the non-linearities.. or you can just pretend that it holds and accept the first estimate. If you want, you can also swap an alternative linearization in place of the truncated taylor (say use my "cheap" method). Unfortunately we still need a new matrix every time we change the linearization.

Now, you don't really HAVE to use a linearization like that. Instead you can approximate f(x1) with something like f(x0) + (x1 - x0)*f'(c) for some fixed c, so you no longer need to recalculate the matrix for each iteration [footnote: apparently in some disciplines it's also common to calculate the first approximation with Newton, then fix that approximation as the constant derivative and refine with fixed-point.. but doing it that way you do need a whole lot more iteration for the same accuracy, so it only ever makes sense when the function evaluations are much cheaper than updating the Jacobian].

Finally at the ultimate end of "as cheap as possible" we get the version that uses the above formula (with fixed derivative-point) and simply accepts the first approximation. I suppose it can be considered a consistent method, since I suppose it should approach the right thing if you take the step-size to the limit at zero... but for any reasonable step-size I wouldn't really expect too much from the accuracy side. I'm not exactly sure (I really don't care enough to figure out) if it's stable (I suspect it's not) without additionally clipping the state-variables (which isn't the right thing to do, but is kinda known to work anyway).

Anyway, the non-linear stuff is orthogonal with the integration methods, and while some combinations might make more sense from the computation point of view, there's no reason you can't combine them in any way you like.

[raphx]

@Z1202: Yes, there is a reasonably simple analytic solution, I posted it about a week ago. Note that this incidentally also gives a closed-form equation for the impulse response, as well. It's not clear to me whether it's slower or faster than the numeric solution, as it has a few (fairly vanilla) function evaluations in it: a sine, a cosine, two exps, and pow(, -0.25).

@mystran: Of course, Newton is a great technique for solving equations, but I prefer straight-through evaluations for audio rate stuff running on phones, where available.

In any case, the spectra of the self-oscillating case look clean, and almost identical in the 2x and 4x oversampling cases, suggesting that it converges.



Incidentally, your solution is not that different - at 1x, it loses a little energy in the high and (and doesn't alias as much, as a result), but at 2x it's basically identical. I'm considering checking in my test rig, so other people can duplicate the experiments if they like.

In other news, I actually have the NEON filter running (but with parameter update still in scalar C), so should be able to do some real performance evaluation of it soon. I'm encouraged, as it's still quite a small number of assembler instructions.

[mystran]

@mystran: Of course, Newton is a great technique for solving equations, but I prefer straight-through evaluations for audio rate stuff running on phones, where available.

Yes, I do understand that, but IMHO it's also important to understand the limitations of each approach. It's perfectly sensible to avoid iterative methods when you don't have the CPU budget, but at the same time I'm objecting to the idea that iterative methods are something you only need for methods that are somehow broken, when in fact you typically need them whenever the accuracy is insufficient otherwise, and the existence of an analytic solution (when ever that happens) is usually pretty much just a "happy accident".

Incidentally, your solution is not that different - at 1x, it loses a little energy in the high and (and doesn't alias as much, as a result), but at 2x it's basically identical. I'm considering checking in my test rig, so other people can duplicate the experiments if they like.

Well, that old method of mine gives you the wrong results by design; it's just one possible answer to the question "if the results are going to be wrong anyway (because we don't want to iterate), how can we make them wrong in such a way that the result doesn't sound too ugly." At low-frequencies and low-gain it's not necessarily that bad, but for anything else it's really just "damage control." It's not about being more accurate, rather about being less ugly (avoid over-estimating IMD, avoid totally ridiculous results, etc).

[raphx]

mystran: Oh, I'm not criticizing your approach at all, in fact I think having a little bit of lowpass on just the nonlinearities is very clever and sophisticated. If you need to update the parameters at audio rate, it's probably the best solution out there (although I'm pushing on my matrix exponential approximation to see how fast I can make it). I'm also not criticizing Newton methods in general either - I've used them very extensively in my other work, including my PhD.

My perspective is that we can boil the whole debate down to a tradeoff between quality and CPU time. One of the most important factors affecting quality (and also CPU, of course) is the degree of oversampling. None of the approaches are all that great at 1x, because high frequencies in the input will get aliased. At higher degrees of oversampling, all three approaches get quite good, fast.

Other factors affecting quality have to do with the accuracy of the (linear) frequency response, and the more complex and subtle terms affecting the accuracy of the nonlinear ODE solving. These also get better in all three approaches as the degree of oversampling goes up.

Long story short, I think the quality is comparable across all three versions for any given oversampling factor. I'm happy to post my test implementation and audio samples so people can verify this claim.

For the linear-only case, I do claim that the matrix exponential approach gives more accurate frequency response than TPT, and that 1x oversampling is adequate. But TPT is still not bad, probably good enough for practical use. (and this is for the lowpass ladder filter case - for highpass, the tables are turned).

I do finally have performance numbers for the audio loop. On my Nexus 10, the linear version runs in 22.5 cycles per sample, and nonlinear in 62 cycles. The latter is calculating five 1/sqrt(1+x*x) sigmoids with adjustable distortion gain, and uses a Newton step to refine the original VRSQRTE approximation. I think these numbers validate my claim that the matrix approach yields incredibly high performance when carefully implemented in SIMD.

As I mentioned, I'm continuing to tweak the matrix exponential optimizations. Since the matrices are Toeplitz, you can cut the number of multiplications about half. I hope to have numbers before too long, but won't have quite as much time to work on this in the coming few days as I had.

[raphx]

I coded up the matrix exponentiation in Neon, and am happy with it. It's 580 cycles on Nexus 10 to compute a matrix, using a fixed 4th order series expansion followed by 4 repeated squarings.

To put this in perspective, if you're running at 1x oversampling and updating every 64 samples, you could run 143 linear filters or 63 nonlinear filters while keeping the CPU clock at a cool 200MHz. Alternatively, if you were maxing out the quality, you should be able to update the matrix every sample and do 8x oversampling and still only consume 1/4 of the 200MHz budget.

The code is checked in if anyone wants to play with it. https://code.google.com/p/music-synthes ... 755ea1e7f3

I also checked in my script for generating audio samples for the various filters: https://code.google.com/p/music-synthes ... sawtest.py

I believe this implementation is competitive with anything out there, although for updating at audio rate I think a careful SIMD implementation of the mystran algorithm, running 4 polyphonic signals concurrently, will no doubt do better for some combinations of oversampling and parameter update rate.

[sonigen]

I do finally have performance numbers for the audio loop. On my Nexus 10, the linear version runs in 22.5 cycles per sample, and nonlinear in 62 cycles. The latter is calculating five 1/sqrt(1+x*x) sigmoids with adjustable distortion gain, and uses a Newton step to refine the original VRSQRTE approximation. I think these numbers validate my claim that the matrix approach yields incredibly high performance when carefully implemented in SIMD.

I'll be honest in that I don't really understand the state space thing but from your first post I got the impression that your method essentially squares a 4x4 matrix 8 to 10 times, for each sample? I really cant see how you could do that in 22.5 cycles.

To square a 4x4 once you have 16 dot products, and then you still have to pack that all back into the matrix to use it again. I don't know about ARM, but on x86 you'll be looking at about 50 cycles to do that once, if you have SSE4, more if you dont.

Edit regards your last post: Looks like i have misunderstood and the matrix exponentiation only happens every 64 samples? When you update the filter parameters?