For the purposes of this question, "trajectory" refers to a path, together with a function r(t) that gives the rate of movement along that path over time.
For simplicity (and I think without loss of generality?), let's consider only systems of 1st-order differential equations (diffeqs).
Let's say you have a system of diffeqs in 2 variables, and it has its flow and trajectories and all that. Certain things like mixing and folding can't happen like they can with 3 variables, because flows in 2 dimensions are constrained in a certain way. So if you project the trajectory of a strange attractor in 3 dimensions down onto a plane, it's likely to cross itself in ways you wouldn't see in a 2-variable system.
So I wonder, if you were to do the same with a 4-variable system, is it possible you might see some sort of behavior in the projection that you would never see in the projection of a 3-variable trajectory? What about more than 4?
(Also, how might one phrase this question rigorously?)
Effect of degrees of freedom on trajectories in dynamical systems
-
- KVRist
- Topic Starter
- 499 posts since 11 Jul, 2004 from Southern California, USA
-
- Banned
- 12368 posts since 30 Apr, 2002 from i might peeramid
think i posted an "oscillator" produced by 3d rotation a week or so back in this forum.. using a constant angle of rotation i was not able to produce a signal more spectrally complex than 8 frequencies. that's 7 more than a 2d rotation..
i'm not really sure about "dynamical" though.. is this discretised from "dynamic"
i'm not really sure about "dynamical" though.. is this discretised from "dynamic"
you come and go, you come and go. amitabha neither a follower nor a leader be tagore "where roads are made i lose my way" where there is certainty, consideration is absent.
-
- KVRAF
- 7893 posts since 12 Feb, 2006 from Helsinki, Finland
edit: Actually, forget what I said, clear you are referring to some implied restrictions/assumptions and I'm just not picking those up for whatever purpose.
-
- KVRist
- Topic Starter
- 499 posts since 11 Jul, 2004 from Southern California, USA
OK, I had a feeling I wasn't being clear enough. My bad.
Motivation:
We model analog circuits with systems of diffeqs. They often have more than three degrees of freedom, but I suspect that every one could be reduced to three variables with the proper selection of functions, and the reason why we use larger systems is because they're a direct result of modeling the circuit, and thus easier to understand.
But I'm not certain this is true. The following is how I'm trying to get a somewhat rigorous handle on the problem.
Problem:
(I could put the following exposition in terms of 1-, 2-, and 3-D systems -- it would be equivalent and directly related to the motivating problem -- but the 2- 3- 4- description is easier to illustrate.)
Here are some flows in two dimensions with selected trajectories drawn. These flows represent systems of two 1st order diffeqs. You'll see that the trajectories never cross themselves. They *can't* if the system is time-invariant (except in some very unlikely cases).
Now here is a trajectory for a particular system in three dimensions.
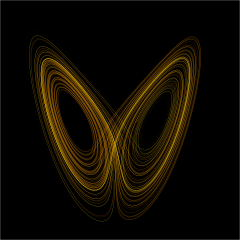
The system is time-invariant (TI), so the trajectory can't cross itself, but it *appears* to because it's been projected onto a plane, that plane being the screen of your monitor. This is an example of interesting behavior that a projection from three dimensions can have.
Now consider a 4-D system with a trajectory that follows the surface of a Klein bottle
where the winding numbers are irrational (the upshot being that the trajectory will come arbitrarily close to any point on the surface of the bottle, given enough time, thereby "covering" the surface).
If you project that trajectory into 3-space, it will appear to cross itself. Now project *again* into 2-space. You'll see a figure-eight blob of curves that all cross each other like mad.
Now here's the thing. There's an irregular torus, and a "covering" trajectory on that torus that doesn't cross itself, with the *same* projection into 2-space. And because it doesn't cross itself, we can devise a 1st-order TI three-variable system for which that 3-D trajectory is a solution. We might guess that all 2-space trajectories have non-self-intersecting 3-D pre-images, which means that *self-intersection in two dimensions can always be "corrected" by "pulling" parts of the trajectory into the third dimension, and it can always be done in such a way that the result is a solution of some three-variable TI system of 1st-order diffeqs*.
So my question is, is there a property of 2-space trajectories that *can't* be so "corrected" by extension into one extra dimension -- is there a property that requires two or more extra dimensions to be "corrected"?
Motivation:
We model analog circuits with systems of diffeqs. They often have more than three degrees of freedom, but I suspect that every one could be reduced to three variables with the proper selection of functions, and the reason why we use larger systems is because they're a direct result of modeling the circuit, and thus easier to understand.
But I'm not certain this is true. The following is how I'm trying to get a somewhat rigorous handle on the problem.
Problem:
(I could put the following exposition in terms of 1-, 2-, and 3-D systems -- it would be equivalent and directly related to the motivating problem -- but the 2- 3- 4- description is easier to illustrate.)
Here are some flows in two dimensions with selected trajectories drawn. These flows represent systems of two 1st order diffeqs. You'll see that the trajectories never cross themselves. They *can't* if the system is time-invariant (except in some very unlikely cases).
Now here is a trajectory for a particular system in three dimensions.
The system is time-invariant (TI), so the trajectory can't cross itself, but it *appears* to because it's been projected onto a plane, that plane being the screen of your monitor. This is an example of interesting behavior that a projection from three dimensions can have.
Now consider a 4-D system with a trajectory that follows the surface of a Klein bottle
where the winding numbers are irrational (the upshot being that the trajectory will come arbitrarily close to any point on the surface of the bottle, given enough time, thereby "covering" the surface).
If you project that trajectory into 3-space, it will appear to cross itself. Now project *again* into 2-space. You'll see a figure-eight blob of curves that all cross each other like mad.
Now here's the thing. There's an irregular torus, and a "covering" trajectory on that torus that doesn't cross itself, with the *same* projection into 2-space. And because it doesn't cross itself, we can devise a 1st-order TI three-variable system for which that 3-D trajectory is a solution. We might guess that all 2-space trajectories have non-self-intersecting 3-D pre-images, which means that *self-intersection in two dimensions can always be "corrected" by "pulling" parts of the trajectory into the third dimension, and it can always be done in such a way that the result is a solution of some three-variable TI system of 1st-order diffeqs*.
So my question is, is there a property of 2-space trajectories that *can't* be so "corrected" by extension into one extra dimension -- is there a property that requires two or more extra dimensions to be "corrected"?
-
- KVRAF
- 7893 posts since 12 Feb, 2006 from Helsinki, Finland
Without additional restrictions, you need at most one variable in addition to the variables you want to observe: introduce additional variable p = p(0) + t (or as differential equation: dp/dt = 1). Now you can encode arbitrary trajectory for x by introducing dx/dt = f(p) where the function f:R->R that encodes the desired trajectory as a function of time: we have turned a time-invariant system into a time-variant one by explicitly introducing time as a system variable. Similar function can then be added for each of the variables you wish to observe.
This result is obviously not helpful in terms of actually computing f, but answers the question on abstract level, doesn't it?
edit: if you want to specify the initial values, you can simply pass those to the function f as additional parameters; it makes f "even less computable" but in the abstract sense it works
This result is obviously not helpful in terms of actually computing f, but answers the question on abstract level, doesn't it?
edit: if you want to specify the initial values, you can simply pass those to the function f as additional parameters; it makes f "even less computable" but in the abstract sense it works
-
- KVRist
- Topic Starter
- 499 posts since 11 Jul, 2004 from Southern California, USA
I'm learning little-by-little how to phrase this question more clearly and succinctly. You still don't understand, which is totally my fault. (Or maybe I don't understand your answer.)
OK: Consider a time-variant function u:R -> R^n and a time-invariant function F:R^n -> R^n, with n>3, such that du/dt = F(u). Let's also name a function v:R -> R^3.
u and v have multiple elements, each expressible as an independent function of t. Take the 0th elements u0 and v0. Is it ever impossible to find a time-invariant function G:R^3 -> R^3 such that dv/dt = G(v) and u0(t) = v0(t)?
OK: Consider a time-variant function u:R -> R^n and a time-invariant function F:R^n -> R^n, with n>3, such that du/dt = F(u). Let's also name a function v:R -> R^3.
u and v have multiple elements, each expressible as an independent function of t. Take the 0th elements u0 and v0. Is it ever impossible to find a time-invariant function G:R^3 -> R^3 such that dv/dt = G(v) and u0(t) = v0(t)?
-
- KVRAF
- 2357 posts since 24 Nov, 2012
I hope I am not being too silly here as it is along time since I looked at dynamical systems but I think Takens theorem covers this http://en.wikipedia.org/wiki/Takens%27_theorem
The wikipedia links to Packard et al and I think the Tim Saeur are good (been along time since I did this stuff)
but from memory the answer to your "So my question is, is there a property of 2-space trajectories that *can't* be so "corrected" by extension into one extra dimension -- is there a property that requires two or more extra dimensions to be "corrected"?" is No
Think of it like this - imagine a plane where every point is 'filled' - a filled black square. Now explode the points into 3 dimensions such that each point is no longer touching any other. All possible trajectories are covered
The wikipedia links to Packard et al and I think the Tim Saeur are good (been along time since I did this stuff)
but from memory the answer to your "So my question is, is there a property of 2-space trajectories that *can't* be so "corrected" by extension into one extra dimension -- is there a property that requires two or more extra dimensions to be "corrected"?" is No
Think of it like this - imagine a plane where every point is 'filled' - a filled black square. Now explode the points into 3 dimensions such that each point is no longer touching any other. All possible trajectories are covered
-
- KVRAF
- 2357 posts since 24 Nov, 2012
i probably should mention that if you are thinking of reconstructing trajectories from a time series then an embedding into df+1 dimensions is required using the delay time embedding method from Packard et-al, Theiler and others .
-
- KVRist
- Topic Starter
- 499 posts since 11 Jul, 2004 from Southern California, USA
OK, Takens' Theorem is interesting. It puts the maximum at ceil(2d) where d is the box counting dimension of the trajectory. Of course the actual value can be less than that, as is the case for many strange attractors, but Takens' Theorem doesn't put further constraints on the answer.
Is there a strange attractor with dimension >= 2.5?
Is there a strange attractor with dimension >= 2.5?
All this says is that every 2-D trajectory has a 3-D pre-image. It doesn't really say anything about what properties the image might have that the pre-image lacks. Or do I misunderstand?Think of it like this - imagine a plane where every point is 'filled' - a filled black square. Now explode the points into 3 dimensions such that each point is no longer touching any other. All possible trajectories are covered.
No that's OK. I'm interested in emulation, not identification.i probably should mention that if you are thinking of reconstructing trajectories from a time series then an embedding into df+1 dimensions is required using the delay time embedding method from Packard et-al, Theiler and others.
-
- KVRAF
- 2357 posts since 24 Nov, 2012
absolutely there are high dimensional attractors - a google search finds heaps of articles
I'm probably misunderstanding what you want as well but you can't reconstruct or emulate the system if all you have is the 2d image and that image has points that are superimposed - eg the crossovers in your Lorenz example above. If that was the data you had then any number of systems could generate that.
as far as my imagining goes - not sure what you are wanting - I think it works in both directions - there is no information in a 2D representation that can't be translated into a 3D representation. Where would that information be hiding? If in the structure of the 2D shape ie the shape as some sort of vector or flow, then it isn't 2D anymore but 3D with a hidden parameter eg time. Any 2d image can have a 3d representation that is the same as the 2d one anyway ie one dimension is set to a constant. Or can have various homeomorphisms in 3d. Any trajectory in 2d can be reconstructed in 3d (I thought my imagined example showed that) but that is just because a trajectory map in 2d (eg the Lorenz again) is really a 3d object collapsed along time. If you can't recover time then you can't recover the original. The 2d image could have all sorts of properties the 3d one doesn't eg intersections but you won't be able to unfold those in 4d if you haven't even got the info to unfold them in 3d. Maybe there are some topological properties that can 'jump' dimensions but that is way outside my knowledge.
I'm probably misunderstanding what you want as well but you can't reconstruct or emulate the system if all you have is the 2d image and that image has points that are superimposed - eg the crossovers in your Lorenz example above. If that was the data you had then any number of systems could generate that.
as far as my imagining goes - not sure what you are wanting - I think it works in both directions - there is no information in a 2D representation that can't be translated into a 3D representation. Where would that information be hiding? If in the structure of the 2D shape ie the shape as some sort of vector or flow, then it isn't 2D anymore but 3D with a hidden parameter eg time. Any 2d image can have a 3d representation that is the same as the 2d one anyway ie one dimension is set to a constant. Or can have various homeomorphisms in 3d. Any trajectory in 2d can be reconstructed in 3d (I thought my imagined example showed that) but that is just because a trajectory map in 2d (eg the Lorenz again) is really a 3d object collapsed along time. If you can't recover time then you can't recover the original. The 2d image could have all sorts of properties the 3d one doesn't eg intersections but you won't be able to unfold those in 4d if you haven't even got the info to unfold them in 3d. Maybe there are some topological properties that can 'jump' dimensions but that is way outside my knowledge.
-
- KVRist
- Topic Starter
- 499 posts since 11 Jul, 2004 from Southern California, USA
There are attractors in high-dimensional systems, but are there attractors with high box-counting or Hausdorff dimension? I can't find any.absolutely there are high dimensional attractors - a google search finds heaps of articles
I should have explained this at the very beginning.I'm probably misunderstanding what you want as well...
Inspired by the use of diffeq systems to model analog circuits, I want to explore these systems and their effects on audio.But: I don't want to explore circuits. I want to explore mathematical systems, whether they're physically realizable or not. Circuits are the inspiration and nothing more.
The more I can limit the search space without loss of generality, the better. So I consider the reasonable speculation that I can stick to 3-dimensional systems, because in 3-space it's easy for trajectories to avoid self-intersection.
So yeah, I'm not interested in system identification, so this isn't a problem.but you can't reconstruct or emulate the system if all you have is the 2d image and that image has points that are superimposed...
-
- KVRAF
- 2357 posts since 24 Nov, 2012
[edit ] OOPs - i see you are only interested in the maths so the following is probably irrelevant again...........
I'm no longer an academic so have limited access but this might be a good starting point on limits on dimension http://link.springer.com/article/10.100 ... 013-0953-1
from memory the statistics of higher dimensional systems are indistinguishable from noise past a certain point (which I can't remember) so probably not useful anyway.
The common musical use as an oscillator has been Chua's I think, but there is long history that I am sure you are already plugged into (going back at least to Mayer-Kress http://www.ee.berkeley.edu/~chua/papers ... ress93.pdf)
Some of the work on control of chaotic systems may be of interest - pushing the attractor around rather than just generating a signal and filtering. (I can still remember the excitement I felt when I first read this paper (and subsequent work) http://www.tufts.edu/~cborgers/CHAOS_PA ... Schiff.pdf )
If you don't know the control literature Grebogi is a good name to start with.
thanks for raising this - I haven't looked at this stuff for over a decade and your post has me interested again
I'm no longer an academic so have limited access but this might be a good starting point on limits on dimension http://link.springer.com/article/10.100 ... 013-0953-1
from memory the statistics of higher dimensional systems are indistinguishable from noise past a certain point (which I can't remember) so probably not useful anyway.
The common musical use as an oscillator has been Chua's I think, but there is long history that I am sure you are already plugged into (going back at least to Mayer-Kress http://www.ee.berkeley.edu/~chua/papers ... ress93.pdf)
Some of the work on control of chaotic systems may be of interest - pushing the attractor around rather than just generating a signal and filtering. (I can still remember the excitement I felt when I first read this paper (and subsequent work) http://www.tufts.edu/~cborgers/CHAOS_PA ... Schiff.pdf )
If you don't know the control literature Grebogi is a good name to start with.
thanks for raising this - I haven't looked at this stuff for over a decade and your post has me interested again
