mutliband-crossover IIR-design with allpass-sum?
- KVRAF
- 4021 posts since 7 Sep, 2002
You need all-pass if crossover points are close to each other. If it's 2-4 or more octaves, I would not even care - the deviation from flat frequency response is negligible, and all you get is some virtual excellence.
Also be careful with all-pass placement - this is important for dynamics processing, because if you apply all-pass after dynamics processing, you'll get deviation, because dynamics adjustment was applied to a relatively shifted response: so, all-pass should be applied first.
Also be careful with all-pass placement - this is important for dynamics processing, because if you apply all-pass after dynamics processing, you'll get deviation, because dynamics adjustment was applied to a relatively shifted response: so, all-pass should be applied first.
-
Music Engineer Music Engineer https://www.kvraudio.com/forum/memberlist.php?mode=viewprofile&u=15959
- KVRAF
- Topic Starter
- 4292 posts since 8 Mar, 2004 from Berlin, Germany
yes, you are right. the deviation from flat frequency response is indeed very small unless there are high-order filters operating close to each other (in which case, in my experience, notches appear). this is probably the main reason why i overlooked this flaw for so long. but still i think, a flaw it is, if a minor one. things like these tend to itch me nonetheless.Aleksey Vaneev wrote:You need all-pass if crossover points are close to each other. If it's 2-4 or more octaves, I would not even care - the deviation from flat frequency response is negligible, and all you get is some virtual excellence.
it is. in my case, it can't be any other way anyway since the plugin i'm talking about is a pure crossover which by itself does not do the summing back.all-pass should be applied first
-
- KVRist
- 48 posts since 17 Aug, 2012 from United States
I was having phase issues while trying to implement this and from the discussion I understood that it could be solved by all-passing the bottom frequency band, but it took me a really long time to figure out what kind of all-pass filter to use. After re-reading and pulling my hair out and consulting with rs-met, I finally realized that it's just a high-pass and a low-pass Linkwitz-Riley Filter (LRF) added in parallel. Here's a schematic to help anyone trying it in the future. Many thanks to everyone on this thread:
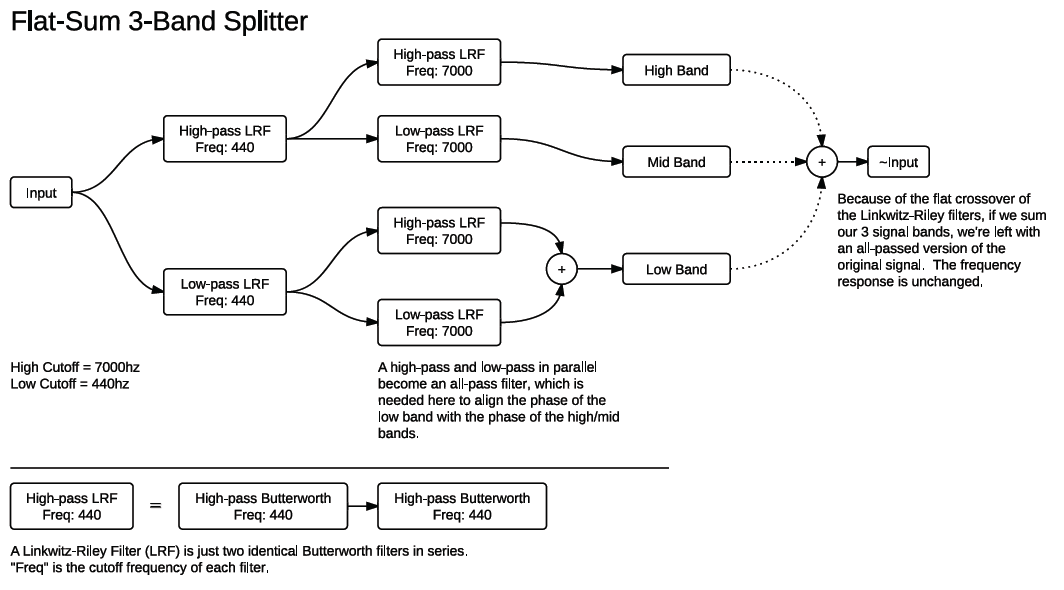

-
Music Engineer Music Engineer https://www.kvraudio.com/forum/memberlist.php?mode=viewprofile&u=15959
- KVRAF
- Topic Starter
- 4292 posts since 8 Mar, 2004 from Berlin, Germany
yes - conceptually, this is the way to go: just make sure, that the low band must go through the same allpass as the (re-combined) high-band. you can apparently do that, by simply letting the low band pass through a second linkwitz/riley splitter (which is a copy of splitter in the high band) and then recombine.Amusesmile wrote:I was having phase issues while trying to implement this and from the discussion I understood that it could be solved by all-passing the bottom frequency band, but it took me a really long time to figure out what kind of all-pass filter to use. After re-reading and pulling my hair out and consulting with rs-met, I finally realized that it's just a high-pass and a low-pass Linkwitz-Riley Filter (LRF) added in parallel. Here's a schematic to help anyone trying it in the future. Many thanks to everyone on this thread:
you can, however, simplify your allpass in the low band by considering, that the parallel linkwitz/riley low- and higpass filters can be combined into a single allpass (so you need to compute only one filter instead of two). moreover, for some reason which i do not yet fully understand, this allpass has only half the order of the original low- (and high-) pass filters, due to pole/zero cancellations. this reduces the computational load by another factor of 2.
- KVRAF
- 7892 posts since 12 Feb, 2006 from Helsinki, Finland
If you add a pair of 2-poles, then in general you would get A(z)/C(z)+B(z)/D(z)=(A(z)*D(z) + B(z)*C(z))/(C(z)*D(z)) which is 4th order, right? But if the poles are the same (ie C(z) = D(z)) then it's simply (A(z)+B(z))/C(z), which is still just 2nd order?Robin from www.rs-met.com wrote:moreover, for some reason which i do not yet fully understand, this allpass has only half the order of the original low- (and high-) pass filters, due to pole/zero cancellations. this reduces the computational load by another factor of 2.
edit: additionally notice that for every set of poles, there is exactly one set of zeroes that will give an all-pass response, so one could just pick any biquad (or more generally any digital filter whatsoever), then form the all-pass zero coeffs by reversing the pole coeffs, and finally solve for the "generalized cross-over pair" by substracting the original filter's zero coeffs from the all-pass coeffs.. then Linkwitz-Riley would be the solution that happens to give "symmetric" filters, no?
-
Music Engineer Music Engineer https://www.kvraudio.com/forum/memberlist.php?mode=viewprofile&u=15959
- KVRAF
- Topic Starter
- 4292 posts since 8 Mar, 2004 from Berlin, Germany
true, but (if i remember correctly), it's not only that the order doesn't double but actually halves. adding the outputs of a 4th order low- and highpass linkwitz/riley filter-pair gives a 2nd order allpass. if A(z)/C(z) is the lowpass butterworth and B(z)/C(z) is the corrsponding highpass butterworth, then (due to squaring of the butterworth response in linkwitz/riley filters) our allpass is given by (A^2(z)+B^2(z))/(C^2(z)). somehow, half of the roots of A^2(z)+B^2(z) seem to automagically coincide with half of the roots of C^2(z), leading to pole/zero cancellations which reduce the order of the allpass by a factor 2. the allpass is actually a (non-squared) butterworth allpass and not a linkwitz/riley (butterworth-squared) one.mystran wrote: If you add a pair of 2-poles, then in general you would get A(z)/C(z)+B(z)/D(z)=(A(z)*D(z) + B(z)*C(z))/(C(z)*D(z)) which is 4th order, right? But if the poles are the same (ie C(z) = D(z)) then it's simply (A(z)+B(z))/C(z), which is still just 2nd order?
disclaimer: it's long ago that i noticed that, so my memory may serve me wrong.
- KVRAF
- 7892 posts since 12 Feb, 2006 from Helsinki, Finland
Let P = 1/(s^2 + s*sqrt(2) + 1).
Let A = P^2, B = (s^2*P)^2.
Then A+B = (s^4 + 1) / (s^2 + sqrt(2)*s + 1)^2.
The denominator has double roots s = -1/sqrt(2) +/- i/sqrt(2)
The nominator has roots s = (-1)^(1/4) * i^n for n in [0,3].
Since (-1)^(1/4) = sqrt(i) = (1 + i)/sqrt(2), two of these cancel a pair of denominator roots, where as the other two are "reflections" across the imaginary axis, hence forming an all-pass pair.
So you're right: the sum has transfer function:
(s - (1 + i)/sqrt(2))*(s - (1 - i)/sqrt(2))
/((s - (-1 + i)/sqrt(2))*(s - (-1 - i)/sqrt(2)))
= (s^2-sqrt(2)*s+1)/(s^2+sqrt(2)*s+1)
Obviously one can get equivalent results on z-plane by using BLT and doing more trigonometry.
edit: I guess this should work with any Linkwitz-Riley order (which is always even) since Butterworth always has poles in a half-circle around origo, so as long as the zeroes always give full circle, half of them will cancel one copy of the half-circle, while the other half will give the "reflection" required for all-pass.
Let A = P^2, B = (s^2*P)^2.
Then A+B = (s^4 + 1) / (s^2 + sqrt(2)*s + 1)^2.
The denominator has double roots s = -1/sqrt(2) +/- i/sqrt(2)
The nominator has roots s = (-1)^(1/4) * i^n for n in [0,3].
Since (-1)^(1/4) = sqrt(i) = (1 + i)/sqrt(2), two of these cancel a pair of denominator roots, where as the other two are "reflections" across the imaginary axis, hence forming an all-pass pair.
So you're right: the sum has transfer function:
(s - (1 + i)/sqrt(2))*(s - (1 - i)/sqrt(2))
/((s - (-1 + i)/sqrt(2))*(s - (-1 - i)/sqrt(2)))
= (s^2-sqrt(2)*s+1)/(s^2+sqrt(2)*s+1)
Obviously one can get equivalent results on z-plane by using BLT and doing more trigonometry.
edit: I guess this should work with any Linkwitz-Riley order (which is always even) since Butterworth always has poles in a half-circle around origo, so as long as the zeroes always give full circle, half of them will cancel one copy of the half-circle, while the other half will give the "reflection" required for all-pass.
-
Music Engineer Music Engineer https://www.kvraudio.com/forum/memberlist.php?mode=viewprofile&u=15959
- KVRAF
- Topic Starter
- 4292 posts since 8 Mar, 2004 from Berlin, Germany
yes, that's the explanation! let me put it into a more general form:
let:
be the lowpass and highpass butterworth transfer functions, where B_N(s) is the N-th order butterworth polynomial. a butterworth polynomial of order N has N roots, defined by the equation 1 + s^2N = 0. these roots occur at -1^(1/2N). this equation has 2N solutions (roots), equally spaced around the unit circle. N of them are in the left half-plane and these are the ones which shall be picked for the N-th order butterworth polynomial.
furthermore, let:
be the allpass obtained by adding a butterworth-squared lowpass and highpass transfer function. this simplifies to:
the denominator still has the left-halfplane roots defined by the equation 1 + s^2N = 0 (as above), but this time, each root has multiplicity 2 (i.e. is a double root). the numerator's roots are defined by the same equation but there's no restriction to pick the left halfplane ones - we use them all. so the every left halfplane numerator root (transfer-function zero) cancels with one denominator root (transfer function pole), leaving a pole with multiplicity 1. and the remaining right halfplane zeros make for the allpass response.
it's automagic!
we can simplfify this allpass transfer function to
where C_N(s) is an N-th order polynomial that has roots defined (again) by 1 + s^2N = 0, but this time with the restriction, that the right halfplane roots should be picked. i don't know whether there's already a name assigned to such polynomials - maybe one could call them "root-reflected butterworth" ...or something.
anyway - i actually did not really add anything substantial to what you said already, just explained it a bit more verbosely, which will hopefully be helpful for someone (including myself when i revisit this topic).
let:
Code: Select all
1 s^N
L(s) = --------, H(s) = --------
B_N(s) B_N(s)
be the lowpass and highpass butterworth transfer functions, where B_N(s) is the N-th order butterworth polynomial. a butterworth polynomial of order N has N roots, defined by the equation 1 + s^2N = 0. these roots occur at -1^(1/2N). this equation has 2N solutions (roots), equally spaced around the unit circle. N of them are in the left half-plane and these are the ones which shall be picked for the N-th order butterworth polynomial.
furthermore, let:
Code: Select all
1^2 (s^N)^2
A(s) = L^2(s) + H^2(s) = ---------- + ----------
B_N^2(s) B_N^2(s)
be the allpass obtained by adding a butterworth-squared lowpass and highpass transfer function. this simplifies to:
Code: Select all
1 + s^2N
A(s) = ----------
B_N^2(s)
the denominator still has the left-halfplane roots defined by the equation 1 + s^2N = 0 (as above), but this time, each root has multiplicity 2 (i.e. is a double root). the numerator's roots are defined by the same equation but there's no restriction to pick the left halfplane ones - we use them all. so the every left halfplane numerator root (transfer-function zero) cancels with one denominator root (transfer function pole), leaving a pole with multiplicity 1. and the remaining right halfplane zeros make for the allpass response.
it's automagic!
we can simplfify this allpass transfer function to
Code: Select all
C_N(s)
A(s) = ---------
B_N(s)
where C_N(s) is an N-th order polynomial that has roots defined (again) by 1 + s^2N = 0, but this time with the restriction, that the right halfplane roots should be picked. i don't know whether there's already a name assigned to such polynomials - maybe one could call them "root-reflected butterworth" ...or something.
anyway - i actually did not really add anything substantial to what you said already, just explained it a bit more verbosely, which will hopefully be helpful for someone (including myself when i revisit this topic).
-
Music Engineer Music Engineer https://www.kvraudio.com/forum/memberlist.php?mode=viewprofile&u=15959
- KVRAF
- Topic Starter
- 4292 posts since 8 Mar, 2004 from Berlin, Germany
btw.: due to the fact that the lowpass and highpass poles are the same, we have the following optimization opportunity:
a naive implementation of a 4th order linkwitz/riley pair would be like this:
where 4p,4z means: the filter has 4 poles and 4 zeros. factoring out the common poles of the lowpass and highpass:
we would have to compute the poles only once for both branches and apply the zeros separately for each branch.
the allpass pole-zero cancellation offers another way to optimize: since AP = LP + HP, we have HP = LP - AP. the allpass has only half the order of the highpass, as explained above. so we could use the half-order allpass instead of the highpass and subtract:
now, we know that the 2 poles of the allpass coincide with the 2 double-poles (a total of 4 poles) of the lowpass, so we may factor out 2 poles once again:
the 4th implementation structure has the smallest operation count. whether this directly translates to less CPU usage should perhaps be measured, however. i'm currently using the 3rd one in my CrossOver. [note to self: for the next update, try the 4th]
i used a 4th order splitter as example - apparently, this works for any order in the same way.
a naive implementation of a 4th order linkwitz/riley pair would be like this:
Code: Select all
--> 4p,4z --> HP
--| 16 poles/zeros to compute
--> 4p,4z --> LP
where 4p,4z means: the filter has 4 poles and 4 zeros. factoring out the common poles of the lowpass and highpass:
Code: Select all
--> 4z --> HP
--> 4p --| 12 poles/zeros to compute
--> 4z --> LP
we would have to compute the poles only once for both branches and apply the zeros separately for each branch.
the allpass pole-zero cancellation offers another way to optimize: since AP = LP + HP, we have HP = LP - AP. the allpass has only half the order of the highpass, as explained above. so we could use the half-order allpass instead of the highpass and subtract:
Code: Select all
--> 2p,2z --> AP ---- + --> HP
| ^
--| *(-1)| 12 poles/zeros to compute
| |
--> 4p,4z --> LP----------> LP
now, we know that the 2 poles of the allpass coincide with the 2 double-poles (a total of 4 poles) of the lowpass, so we may factor out 2 poles once again:
Code: Select all
--> 2z --> AP ---- + --> HP
| ^
--> 2p --| *(-1)| 10 poles/zeros to compute
| |
--> 2p,4z --> LP-------> LP
the 4th implementation structure has the smallest operation count. whether this directly translates to less CPU usage should perhaps be measured, however. i'm currently using the 3rd one in my CrossOver. [note to self: for the next update, try the 4th]
i used a 4th order splitter as example - apparently, this works for any order in the same way.
- KVRAF
- 7892 posts since 12 Feb, 2006 from Helsinki, Finland
Splitting poles first is going to cause precision issues though, especially with direct forms. Then again, if you have a structure (like SVF, or lattice/ladder etc) that can give you multiple zero configs at once, you can do:
This is just two generic biquads. We need multiple responses (AP and LP) for the first one, but observe that you get AP for free if you use a lattice (and ZDF SVF would give LP for "free" and have superior precision, though at higher cost).
Code: Select all
--> AP -----------------+--> HP2
| ^
--> SVF1 -1|
| |
--> LP -> SVF2 -> LP2 -----> LP2













