AUTO-ADMIN: Non-MP3, WAV, OGG, SoundCloud, YouTube, Vimeo, Twitter and Facebook links in this post have been protected automatically. Once the member reaches 5 posts the links will function as normal.
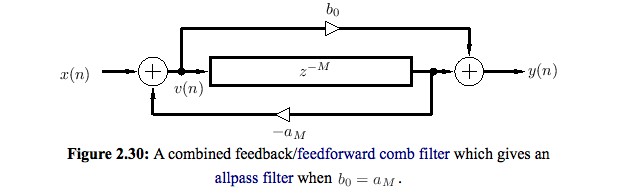
Hello everybody. I experimented with simple classic reverb using combofilter and allpassfilter. Now I want to make a reverb using feedback delay network. I can’t figure out how to create a allpass filter with modulation. This is what i have now. Sorry anti-bot does not allow to place the code
https://www.codepile.net/pile/kwRX48ZQ (https://www.codepile.net/pile/kwRX48ZQ)